Week 1: Thursday

Introduction

Maxim Aleksa '17.
The goal of discussion sections is to review the material covered in lectures, visit new material, as well as advise on homeworks and projects.
Slides, notes, source code, links and all other material will be posted at umich.edu/~maximal/eecs281.

Algorithms

Computer science is not only about programming, but also about computational thinking. In fact, we can distill computer science and computational thinking into these three ideas:

inputs → algorithms → outputs

As we try to process inputs to produce outputs, we need to come up with algorithms that are not only correct, but also efficient, such that we can get answers quickly to problems with large input sizes.
To illustrate how quickly some function might grow, we’ll use an example.

Suppose you could have either
- A million dollars today, or
- One penny today, two pennies tomorrow, four cents the next day, …, for a month.
Though a million dollars might sound good, you should pick the latter option whenever asked to make such decision in life. Since the amount of money you get is doubled each day, the total amount of money you get will outgrow one million dollars before the end of the month, as illustrated by this Excel table.

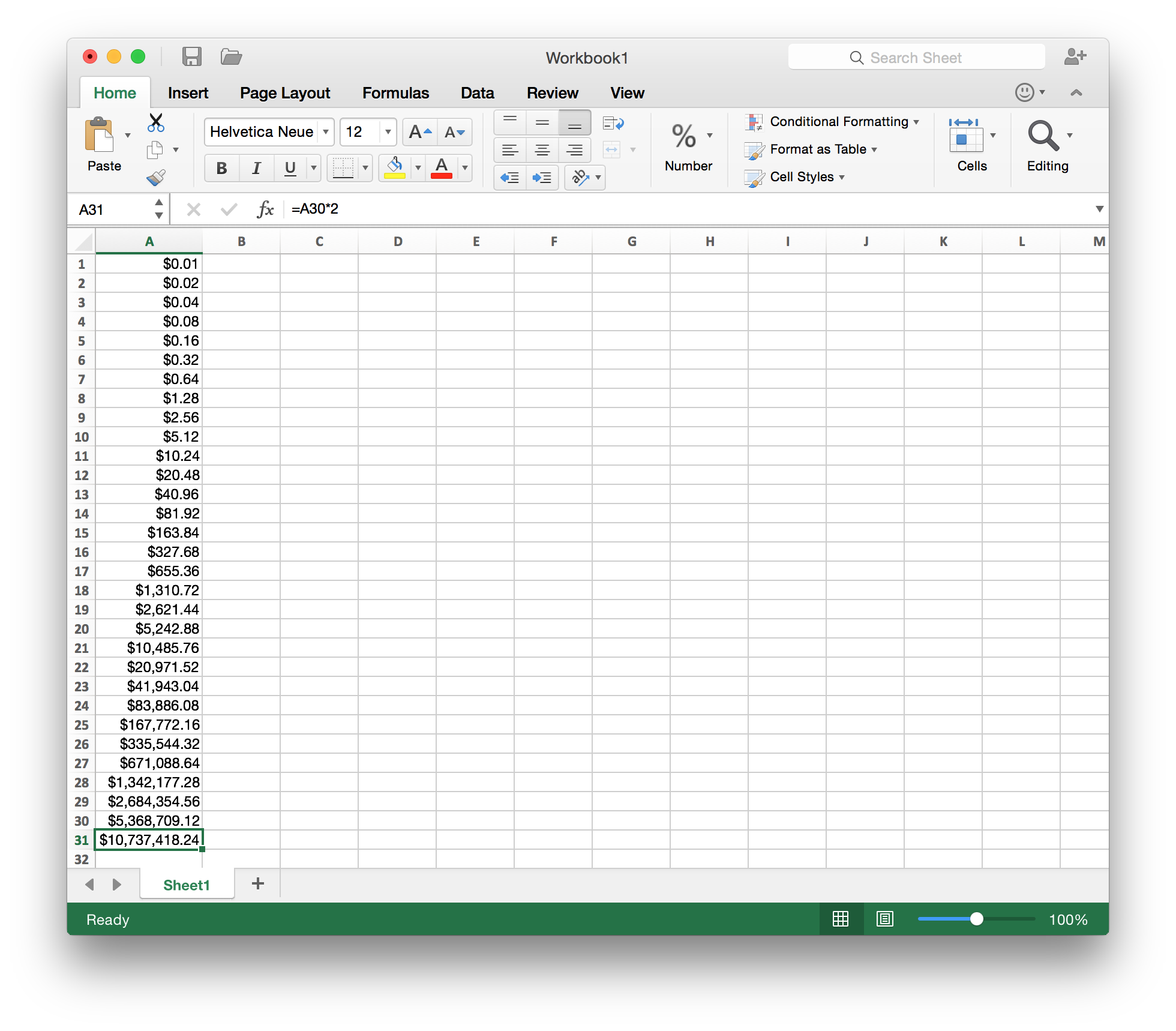
And so when designing algorithms, we should be careful about how much work the computer will have to do for large inputs. We often worry more when an algorithm executes slowly for large inputs than when it executes quickly for small inputs.
But in general, we also should put thought into what the algorithm does and how it does that. If there are any assumptions about the input, we should take advantage of them when we design an algorithm.

Suppose you had to detect if a sorted array A had duplicates. In other words, given a sorted array A, find indices i and j where A[i] = A[j]. The array might look something like this:

-3

-1

2

4

5

8

10

12

One approach could be to create a list of pairs and iterate through all pairs until you find a pair with the same numbers: (-3, -1), (-3, 2), (-3, 4), …, (10, 12). But your instinct should tell you that this is not the most efficient solution. If $N$ is the size of the array, this algorithm would generate $\frac{N^2}{2} - \frac{N}{2}$ pairs. And then you’d have to go through those pairs and look for one with the same numbers. This algorithm would take roughly $N^2$ steps.

A much better algorithm would be to compare each number A[i] with A[i + 1]. We can do this since the array is sorted! This algorithm would take at most $N - 1$ steps.

Take a look at this table that illustrates the running times (rounded up) of different algorithms on inputs of increasing size, for a processor performing a million high-level instructions per second. In cases where the running time exceeds 10²⁵ years, the algorithm is recorded as taking a very long time.[1]

input size	n	n log₂ n	n ²	n ³	1.5ⁿ	2ⁿ	n !
n = 10	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	4 sec
n = 30	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	18 min	10²⁵ years
n = 50	< 1 sec	< 1 sec	< 1 sec	< 1 sec	11 min	36 years	very long
n = 100	< 1 sec	< 1 sec	< 1 sec	1 sec	12,892 years	10¹⁷ years	very long
n = 1,000	< 1 sec	< 1 sec	1 sec	18 min	very long	very long	very long
n = 10,000	< 1 sec	< 1 sec	2 min	12 days	very long	very long	very long
n = 100,000	< 1 sec	2 sec	3 hours	32 years	very long	very long	very long
n = 1,000,000	1 sec	20 sec	12 days	31,710 years	very long	very long	very long

input size

n log₂ n

n ²

n ³

1.5ⁿ

2ⁿ

n !

n = 10

< 1 sec

4 sec

n = 30

< 1 sec

18 min

10²⁵ years

n = 50

< 1 sec

11 min

36 years

very long

n = 100

< 1 sec

1 sec

12,892 years

10¹⁷ years

very long

n = 1,000

< 1 sec

1 sec

18 min

very long

n = 10,000

< 1 sec

2 min

12 days

very long

n = 100,000

< 1 sec

2 sec

3 hours

32 years

very long

n = 1,000,000

1 sec

20 sec

12 days

31,710 years

very long

Asymptotics

When deciding how fast or slow algorithms are, we do not want to solely rely on measurements in seconds, since that is very machine-dependent (you can just buy a new computer next year and your algorithm will execute twice as fast!) and variable (running time is most likely to be different every time you execute the algorithm). Instead, we use Big O notation, the Big Theta Θ and Big Omega Ω notations to describe the order of growth of algorithms.

Name	Big O	Big Omega	Big Theta
Notation	\(f(n) \in O(g(n))\)	\(f(n) \in Ω(g(n))\)	\(f(n) \in Θ(g(n))\)
Informal meaning	Order of growth of \(f(n)\) is less than or equal to \(g(n)\)	Order of growth of \(f(n)\) is greater than or equal to \(g(n)\)	Order of growth of \(f(n)\) is \(g(n)\)
Example family	\(O(N^2)\)	\(Θ(N^2)\)	\(Ω(N^2)\)
Family members	\(\frac{N^2}{2}\), \(2N^2 + 1\), \(\log(N)\)	\(\frac{N^2}{2}\), \(2N^2 + 1\), \(e^N\)	\(\frac{N^2}{2}\), \(2N^2 + 1\), \(N^2 + 183N + 5\)

Name

Big O

Big Omega

Big Theta

Notation

$f(n) \in O(g(n))$

$f(n) \in Ω(g(n))$

$f(n) \in Θ(g(n))$

Informal meaning

Order of growth of $f(n)$ is less than or equal to $g(n)$

Order of growth of $f(n)$ is greater than or equal to $g(n)$

Order of growth of $f(n)$ is $g(n)$

Example family

$O(N^2)$

$Θ(N^2)$

$Ω(N^2)$

Family members

$\frac{N^2}{2}$, $2N^2 + 1$, $\log(N)$

$\frac{N^2}{2}$, $2N^2 + 1$, $e^N$

$\frac{N^2}{2}$, $2N^2 + 1$, $N^2 + 183N + 5$

Let’s consider this code so that we can provide an example for the above notation.
```
int count = 0;
for (int i = 0; i < N; ++i) {
    if (arr[i] == 0) {
        ++count;
    }
}
```
Let’s analyze this code and count how any operations it invokes. There is one assignment (count) before the for loop, plus another one inside (i). The for loop does $N + 1$ comparisons and $N$ updates (so $3 + 2N$ steps so far). On each iteration of the for loop (which executes $N$, we do one comparison and zero or one increments of count. So the total number of operations $R(N)$ is $3 + 3N ≤ R(N) ≤ 3 + 4N$. We can say that the execution time grows in the order of $N$, so the best way to describe the performance of the above snippet of code would be $Θ(N)$. (It is also $O(N)$ and $Ω(N)$.)
Now let’s consider this function.
```
bool hasDuplicates(const int numbers[], int size) {
    for (int i = 0; i < size; i += 1) {
        for (int j = 0; j < size; j += 1) {
            if (numbers[i] == numbers[j]) {
                return true;
            }
        }
    }
    return false;
}
```
What is the order of growth $R(N)$, where $N$ is the size of numbers array?
1. $R(N) \in Θ(1)$.
2. $R(N) \in Θ(N)$.
3. $R(N) \in Θ(N^2)$.
4. Something else.
The correct answer is A. $R(N) \in Θ(1)$. Notice that the very first comparison is numbers[i] == numbers[j] where i and j are both zero. It is always the case that numbers[0] == numbers[0], so the function always returns true in constant time. Notice that even though there are two for loops, the order of growth is $Θ(1)$ and not $Θ(N^2)$.
Let’s fix the bug in hasDuplicates by changing j = 0 to j = i + 1.
```
bool hasDuplicates(const int numbers[], int size) {
    for (int i = 0; i < size; i += 1) {
        for (int j = i + 1; j < size; j += 1) {
            if (numbers[i] == numbers[j]) {
                return true;
            }
        }
    }
    return false;
}
```
Now, what is the order of growth $R(N)$, where $N$ is the size of numbers array?
1. $R(N) \in Θ(1)$.
2. $R(N) \in Θ(N)$.
3. $R(N) \in Θ(N^2)$.
4. Something else.
The correct answer is D. Something else. It might seem that now that we’ve fixed the bug $R(N) \in Θ(N^2)$. But that is only the case when we have to go through the entire array. For some arrays (e.g. an array of all zeros), we only have to compare the first two elements. So if the array contains just zeros, the function will execute in constant time regardless of the size of the array. Since the answer options have Big Theta and not Big O, the answer is something else (depends on the input). It is true, however, that $R(N) \in O(N^2)$.

Project 1

Due by 11:55pm on Tue 5/12, so start soon! Also, Homework 1 is due by 11:55pm on Sun 5/10.
You can view the calendar with office hours on the home page of the course’s website.

getopt

Project 1 (and other projects in EECS 281) will require you to parse command line arguments. These command line arguments have short and long versions (e.g. -h and --help). Command line arguments can be specified in different order and some will have their own arguments (flags). For example, your program should support the following.
```
./ship -h
```
```
./ship --help
```
```
./ship -queue --output M
```
```
./ship -o M -q
```
The getopt function will make our lives much easier.

Begin using getopt by #including <getopt.h> in your code. Next, in the beginning of main list all the command-line arguments your program supports, with a nullptr at the end (in case someone tries to use an illegal argument).

struct option longOpts[] =
{
    {"help", no_argument, nullptr, 'h'},
    {"output", required_argument, nullptr, 'o'},
    {nullptr, 0, nullptr, 0}
};

For each command-line argument, specify its long version, whether or not it requires an argument (with no_argument, optional_argument or required_argument), then say nullptr and finally list the short version as a char.

Then write a while loop that will call get_opt to parse command-line arguments. The third argument of get_opt is a string containing the short versions of command-line arguments. Each is followed by a single colon (:) if it requires an argument and by a double colon (::) if its argument is optional. Access those required or optional arguments with optarg (which is a char *).

char opt;
index = 0;
while ((opt = getopt_long(argc, argv, "ho:", longOpts, &index)) != -1)
{
    switch (opt)
    {
        case 'h':
            // print help message
            break;

        case 'o':
            // decide output
            // get the required argument with optarg
            cout << optarg;
            break;

        default:
            printf("O no! I didn't recognize your flag.\n");
            exit(0);
            break;
    }
}

You can also take a look at the slides in Resources > Lecture > 00a_Workflow.pdf.

Data Structures

Recall queues and stacks.
A queue is a data structure that is similar in spirit to a fair line. As you can see in this photo, the first dog in line can expect to be the first to pee on the tree.
A stack is a data structure that is similar in spirit to a pile of trays or plates in a dining hall. When the dining staff put plates out before meals, they pile them from the bottom to the top, and then you take the top-most plate. The last plate that the staff put on the piles is the first one taken from the pile.
Since Project 1 will involve both queues and stacks, you might first try to create two separate data structures for each. However, it is much easier to maintain just one data structure. STL deque (usually pronounced like deck) allows you to do exactly that. It is a double-ended queue. You can push items to the front and to the end and you can remove items from the front and from the end in constant time.

To use deques, #include <deque> atop your code. Declare a deque of ints with this line of code.
```
deque<int> numbers;
```
After you insert some integers, the deque might look something like this:

…

281

101

183

280

203

381

…

Xcode

If you work on your projects in Xcode, there are a few things you can do to make your life easier.
To pass command-line arguments to your program, head to Product > Scheme > Edit Scheme > Run (on the left) > Arguments (at the top). Click on the plus sign and add any arguments that you want to pass on launch.
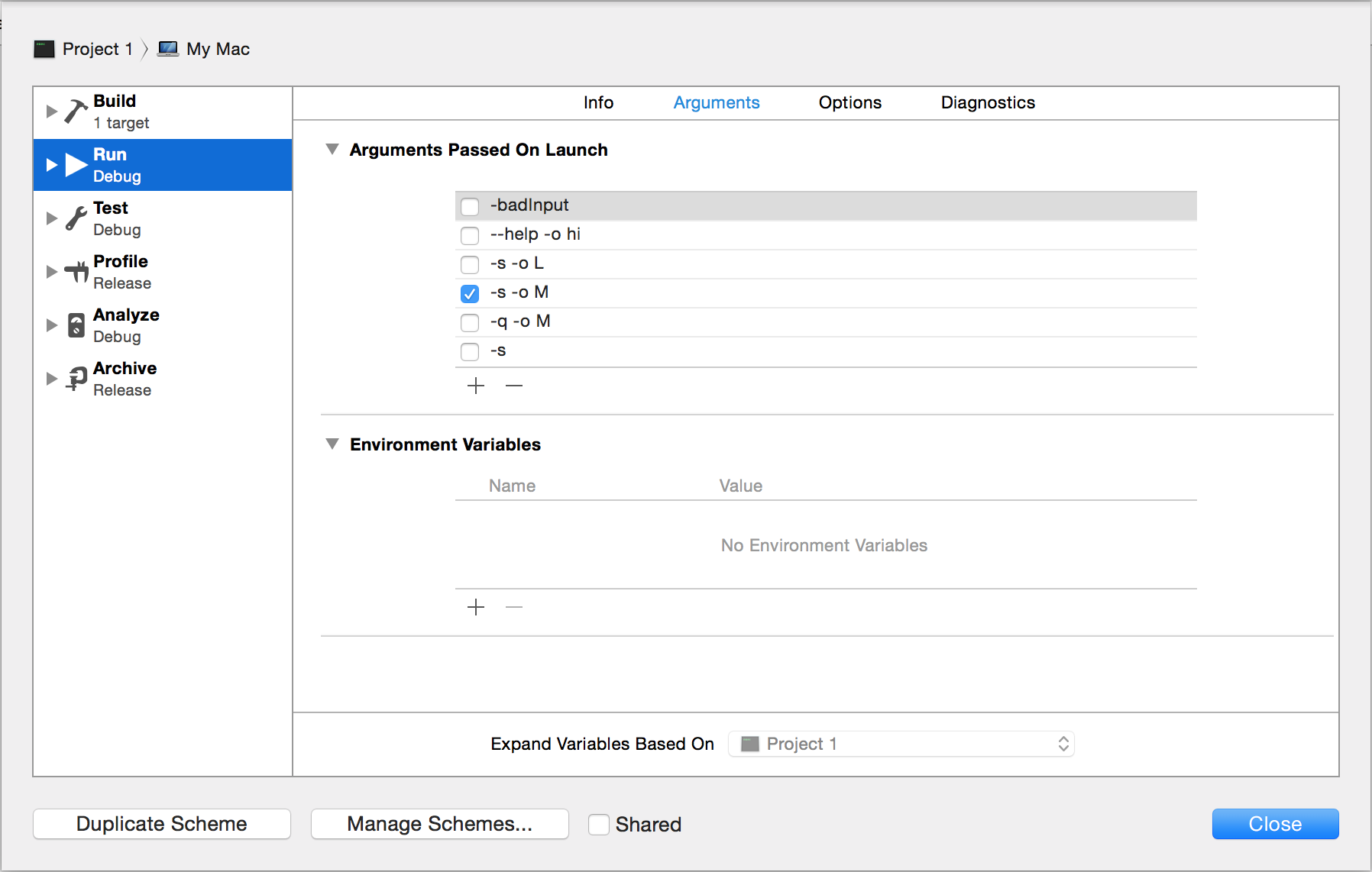
If you don’t want to manually type or copy and paste input into the console, you can redirect input from a file. From the menu bar, select Product > Scheme > Edit Scheme. Then choose Run (on the left) ands Options (at the top) and set the custom working directory to where your input files are located. This will make Xcode look for input files in the correct folder, instead of the directory where it stores the project’s executable. Then add this line of code at the beginning of main to redirect input from input.txt to cin (standard input stream).
```
freopen("input.txt", "r", stdin);
```
Don’t forget to comment this line out before you submit!

Makefile

make is a program (and programming language) intended to help the development of programs that are constructed from one or more source files. For instance, you can execute this command in CAEN environment (if you have hello.cpp in your current directory)
```
make hello
```
which will be equivalent to
```
g++     hello.cpp    -o hello
```
If you execute
```
make hello
```
again (without changing hello.cpp), make will inform you that `hello' is up to date.
As you can see, make provides an easy way to build a program.
We can use make to our advantage and make the build process more complex. We can create Makefiles that specify the relationship between the source files necessary to build a program so that make will execute the correct commands for us. After creating a Makefile in the directory with our source files, we can execute make with different targets to build our program in different ways.

Contents of a Makefile

We can divide the contents of a Makefile in four categories:
Comments

Any line that starts with a # in the first column is a comment and is ignored by make.

Variables
Define variables (macros) like this.
VARIABLE_NAME = value
The above line defines a variable called VARIABLE_NAME whose value is the entire contents of the line after the =, except surrounding whitespace.

Once a variable is defined, it can be extracted with the $(VARIABLE_NAME) operator.

You can use of variables in a Makefile to enable version 4.8.2 of gcc and C++11 on CAEN.
# enables c++11 on CAEN PATH := /usr/um/gcc-4.8.2/bin:$(PATH) LD_LIBRARY_PATH := /usr/um/gcc-4.8.2/lib64 LD_RUN_PATH := /usr/um/gcc-4.8.2/lib64
Dependency rules
Dependency rules are the heart of make. Their purpose is to define the dependency of some target on some sources, to let make know that it needs to have (or make) all the sources before it can make the target. They also let make know that it will need to recreate the target if any of the objects that the target depends upon are more recent than the target.

A dependency rules must start in this form.
target: dependencies action
Derivation rules
Derivation rules tell make how to “automatically” make a file with a particular suffix out of a file with another suffix, you can set up rules that look similar to dependency rules, but do not contain the names of specific files. For example, to tell make to make .o files from .cpp files using the g++ compiler in the same manner as before, you could write:
.c.o: g++ -o $@ $?

EECS 281 Makefile

EECS 281 provides a sample Makefile in Project 0. You are very much encouraged to use this Makefile, since you will need to include one in your submission. The sample Makefile will also facilitate compressing your files into at .tar.gz archive before you submit.
To use EECS 281 Makefile for Project 1, first download the Project 0 archive from Resources and extract the Makefile. Take a look at it and read the comments. Next, search (with Command-F or Control-F) for TODOs that will indicate where you need to modify the sample Makefile. Specifically, you will most likely need to make two changes.
- Set EXECUTABLE to ship for Project 1.
- Set PROJECTFILE to the .cpp file that has the main function.
That’s it! You can use this Makefile for Project 1 (and for the other projects, so long as you remember to change the value of EXECUTABLE).
Once you transfer your project files (including your Makefile) to a directory on CAEN, you’ll be able to execute these commands.
```
make release
make all
make debug
make profile
make clean
make test_class
make alltests
make partialsubmit
make fullsubmit
```
In addition, you’ll be able to execute
```
make help
```
to get information on exactly what each of the commands does.
To submit, execute make fullsubmit for submission of project without test files. Execute make partialsubmit for submission of project without test files. You might want to create partial submission when you are just starting working on your project and do not want to risk losing a submission if your code does not compile. (If your code does not compile and you submit test cases, you will use one submission. If you code does not compile and you do not submit test cases, you will not use one submission.)
You can also take a look at the slides in Resources > Project > Project 0 > make_and_project0.pdf.

1. Adapted from Table 2.1, p. 34 of Jon Kleinberg and Eva Tardos. 2006. Algorithm Design. Pearson Education, Inc.